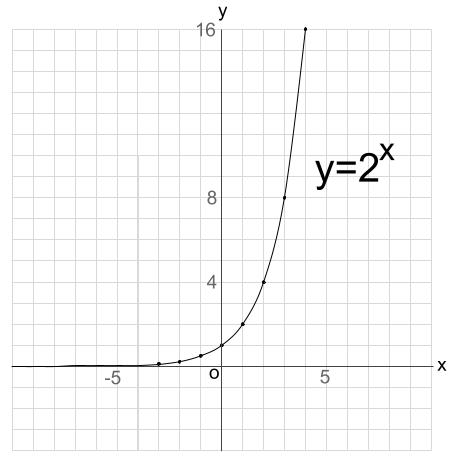
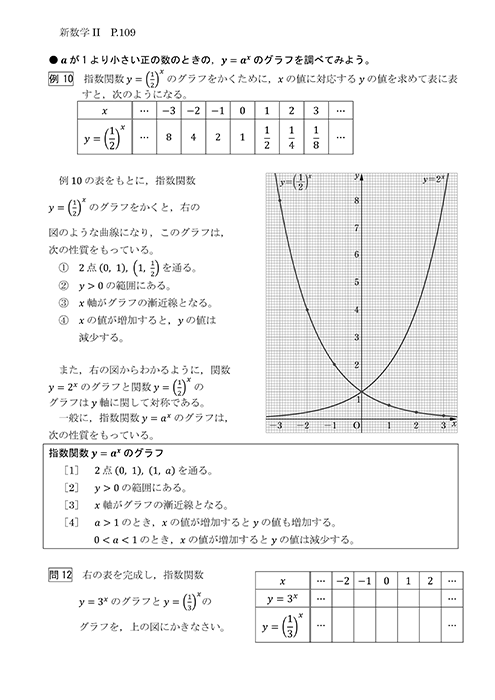
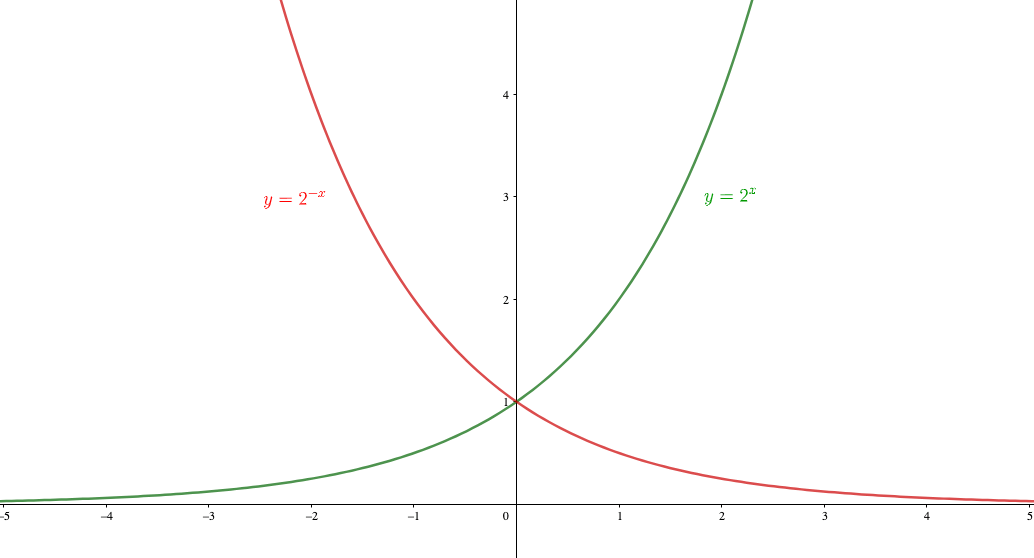
Exp3P1 :3つのパラメータ指数関数(Xの逆数式) Exp3P1Md :3つのパラメータ指数関数(Xの逆数式) Exp3P2 :3つのパラメータ指数関数(Xの二乗式) ExpAssoc : 指数関数の結合 Exponential :指数関数 ExpDec1 :指数減少関数 ExpDec2 :指数減少関数(指数2項の合成漸近線を持つ代表的な関数 漸近線はない場合もありますし、複数ある場合もあります。 ですが漸近線を必ず持つとわかっている関数がいくつかあるので、最低限これらの関数は押さえておきましょう。 指数関数 \(y=2^x,y=2^{x}\)はグラフのようになりますが、\(x\)軸に着目すると漸近線である性質 1 (0,1),(1,a)を通り,x 軸を漸近線とする曲線となる。 性質 2 a>1 のときは増加関数(右上がり),0<a<1 のときは減少関数(右下がり)である。 〈注意〉a>0,a≠1 のとき, r=s ⇔ ar=as が成り立つ。 グラフの平行移動
2
漸近線 求め方 指数関数
漸近線 求め方 指数関数-指数関数とはなにか? 指数関数の重要な性質について(漸近線、底による場合分け) 指数関数のグラフを正しく書く練習問題3選 以上について、わかりやすく丁寧に解説します。 「指数関数がイマイチピンときていない」と感じている方は必見です。有理数(整数や有理数分数)の x ,例えば x= に対して指数関数 a x は累乗根 で定義されますが,指数関数のグラフを書くためには, x= のように x が無理数の場合にも点が描かれていなければ,グラフに穴があいてしまいます.これをどう考えるのかについて. 無理数 x= については,指数関数
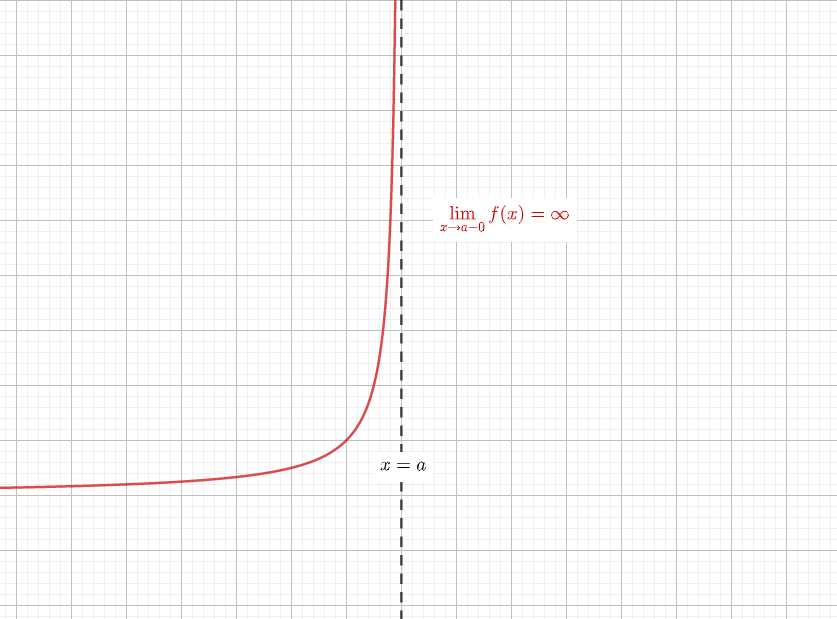



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
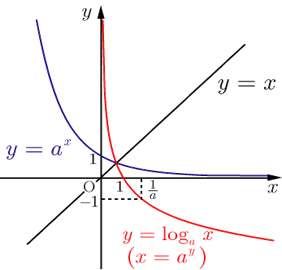
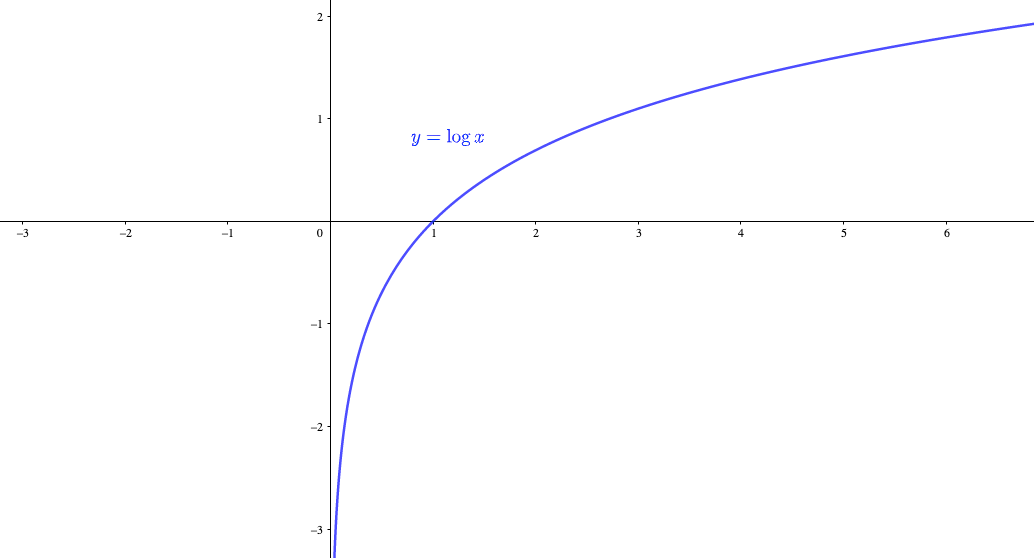
無理関数のグラフの概形、書き方高校数学Ⅲ 指数関数、対数関数のグラフの概形高校数学Ⅲ 三角関数のグラフの概形と書き方高校数学Ⅲ 漸近線とは?求め方高校数学Ⅲ 複雑な関数の概形(偶関数と奇関数)高校数学Ⅲ 37方程式、不等式への応用 実数解の個数の求め方対数関数\(y=\log_a x\)は、 指数関数に直して考えるとわかりやすい。 底\(a\)が1以下の小数か、1以上か場合分けして考える。 底の値によらず、必ず点\((1,0)\)を通る。 \(y\)軸を漸近線にもつ。 指数関数とは、逆関数の関係にある。 対数関数の漸近線の求め方がわかりません。 ス、せ、ソの解説をお願いしたいです🙇♀️ 04。ょ(Jet9) 7 G) 右の図は, 関数 マー logs(x二の上1 のグラフ の一部分であさ請語間軸 このとき ャ c王 の還語 である。 ー1) を通るから 0 apローー ig2ニータ うー の には) こ 2 お 関数 ゞニ
分数関数とは? グラフや微分・積分、不等式の解き方 21年2月19日 この記事では、「分数関数」についてわかりやすく解説していきます。 グラフの書き方や不等式の解き方、微分・積分の計算なども説明しますので、この記事を通してぜひマスターして関数の逆関数であるという 1 逆 関 数 の 関 係 対数関数 y x loga a a 0, 1 特徴 ・点 1, 0 , , 1 a を通る ・y 軸を漸近線とする曲線 ・a 1のとき右上がりの曲線 0 1 a のとき右下がりの曲線 指数関数 y a x a a 0, 1 特徴 ・点 0, 1 , 1, a を通るCovar関数,covariancep関数を使用して共分散を求めてみよう covariancep関数とs関数の違いは?演習問題 excel階乗の計算方法 fact関数で階乗を求めてみよう演習問題 参考文献 excel関数を使わずにデータを間引く方法一定間隔の抽出
これから関数は、 (基本形)のグラフをx軸,y軸の正の方向へそれぞれp,qだけ平行移動したものである。 このときx=p,y=qが漸近線となる。ここで、 のグラフは、直線y=xに関して対称なグラフであるから逆関数も である。 逆関数の漸近線はx=q,y=pより、その方程式は、 となる。漸近線の方程式 解説 高校の微分積分で漸近線の問題が登場するのは,微分法の応用として,「増減,極値,凹凸,変曲点,漸近線の方程式を求めてグラフの概形を書け」という場面です。 したがって,漸近線の方程式を単独で問うことはまれです。 漸近線とはグラフが近づいていく直線(または曲線)のことです。 厳密には極限を用いて定義されますが,一次分数関数に関しては漸近線は極限の議論をしなくても分かります。 さきほどかいた二つのグラフを見れば明らかでしょう。 一次分数関数 y −




指数関数の性質について 数学ii フリー教材開発コミュニティ Ftext



対数関数
数 II 指数関数と対数関数 指数関数とは? グラフや計算公式、微分積分や方程式・不等式 21年2月19日 この記事では、「指数関数」とは何かをわかりやすく解説していきます。 指数関数のグラフや方程式などの計算問題、微分積分の公式なども説明して漸近線の求め方を解説しました。 グラフの漸近線は、x軸に垂直な漸近線とそうでない漸近線とがあります。 そうでない漸近線は、\(x\to\pm\infty\)において漸近線と曲線が限りなく近づきます。 漸近線の方程式を\(y=axb\)とすると、曲線\(y=f(x)\)の漸近線は、 双曲線の漸近線の簡単な求め方と証明 双曲線の漸近線の簡単な求め方と証明 漸近線とは,関数が 原点から遠い部分で限りなく近づく直線 のことです。 まずは具体例から。 例1 x 2 4 − y 2 9 = 1 \dfrac{x^2}{4}\dfrac{y^2}{9}=1 4 x 2 − 9 y 2 = 1 という双曲線の漸近線は,( a = 2, b = 3 a=2,b=3 a = 2, b = 3 とし
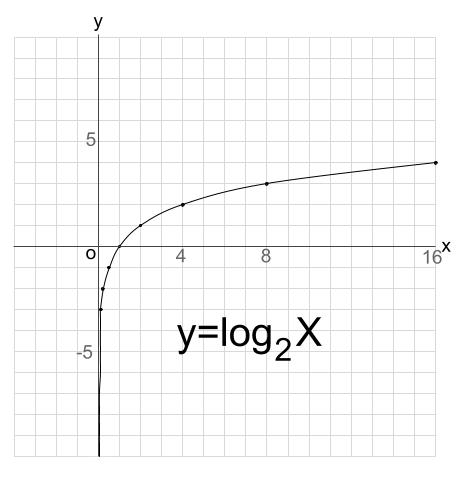



対数関数のグラフ 高校数学の無料オンライン学習サイトko Su
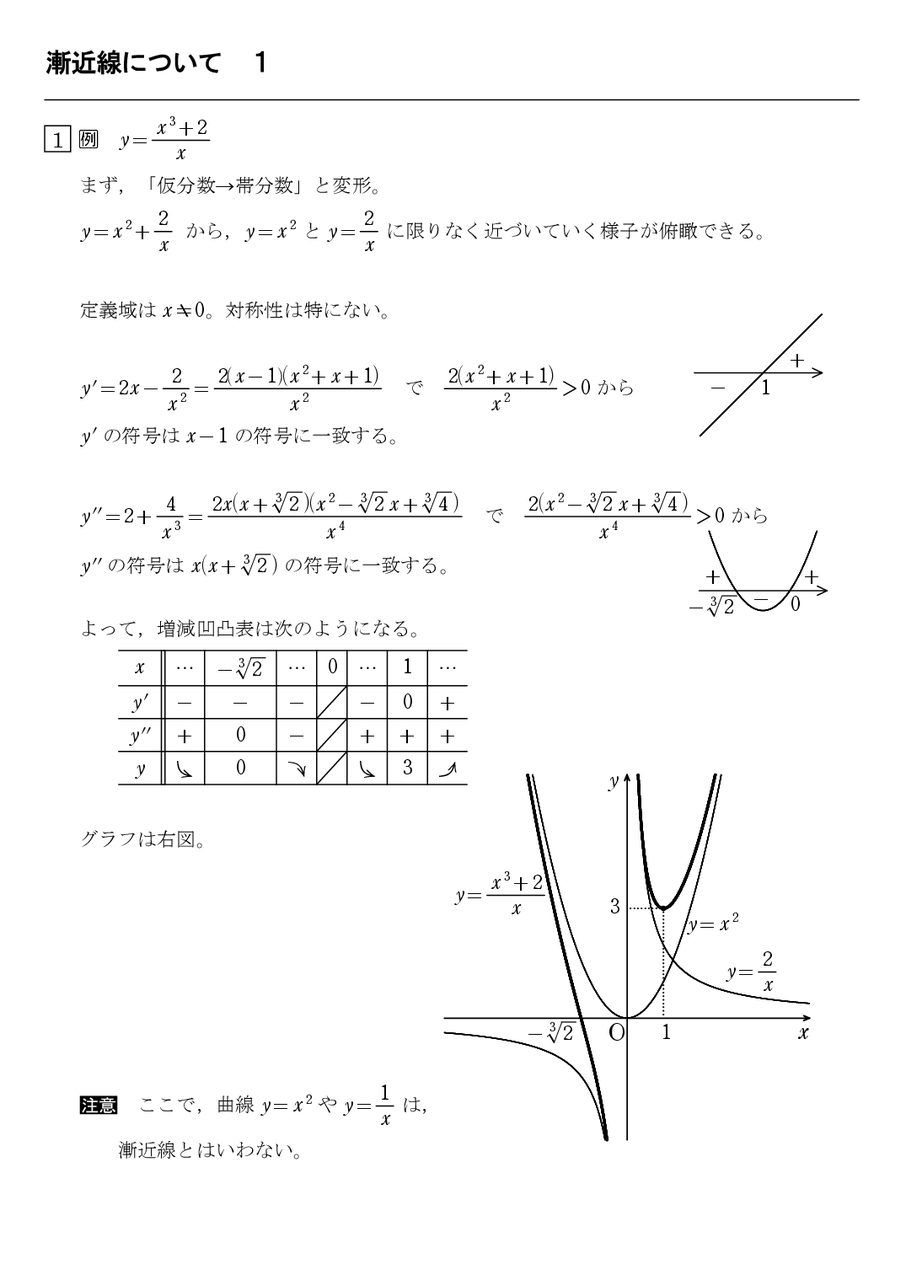



増減凹凸表を書く手順 7 漸近線 1 怜悧玲瓏 高校数学を天空から俯瞰する
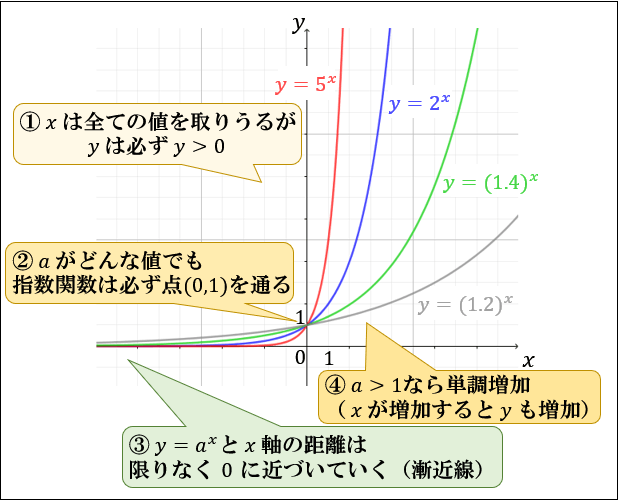
指数関数とは、a > 0 かつ a ≠ 1 のとき「 y = a x 漸近線は \(x\) 軸 \((y=0)\) \(a>1\) なら単調増加(\(x\) が増加すると \(y\) も増加) 円周の求め方・円周率とは何か・なぜ無限に続くのかを説明。その割り切れない理由について 15m件のビュー;※この頁では漸近線の方程式の求め方を解説します. (1) 縦方向の( x 軸に垂直な)漸近線 有限の値 a に対して, x→a のとき y→∞ または y→−∞ になるとき, x=a が漸近線になります. 例11 y= の関数において, x=1 のときは分母が0となって 関数が定義されず, x→1 のとき y→±∞ と 指数関数のグラフ こんにちは! うちやま ( @s_uchiyama_1 ) です。 今回のテーマは 指数関数のグラフ です! 今回の授業内容をざっくりと理解したい人は、まずは下の動画 ()をご覧ください! 気に入ったらチャンネル登録もお願いします! 指数関数




指数関数の意味と性質 グラフ




指数関数を正しく理解して 指数関数のグラフを書いてみよう 遊ぶ数学
指数関数のグラフは上で示したような概形となるのですが、なぜこのような形となるか直感的に理解できる方は 指数法則 をよく理解できていることでしょう。 の場合の指数関数 とを例とし、グラフの概形について代数的に理解しましょう。 の値を順次 単元 積分, 「漸近線の描き方を一目にまとめました。 漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。」, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め方生徒からあった。確かにf( )が微分可能な関数で あれば,直感的には正しそうである(図1参照)。は たして,これは正しいのであろうか。 図1 関数 = −1 のグラフとその漸近線 §2.漸近線の定義 この質問に答えるためには,まず漸近線の定義を 確認する必要がある。教科書には,漸近線の定義は




対数関数のグラフと書き方 数学 理系ラボ




指数 対数関数 グラフ編 ますますmathが好きになる 魔法の数学ノート
漸近線の求め方 y=f(x) の漸近線 が よってx 2は漸近線 分数関数の例2 x3 1 y x のグラフ 3 y x x 1 1 2 x x 0 0 lim , lim x x y y より, 漸近線は直線x 0 また, lim{ } lim 02 1 x x y x x , 2 1 x x y x x より, x のとき 2 2 1 y x x x よってこのグラフは,y x 2 に近づく。 y x 2 y x 2 Title Microsoft Word Ⅲ 03_漸近線 漸近線は、 基本双曲線と漸近線 や 基本一次分数関数のグラフ などでも出てきていますが、このページの後半で、もう少し詳しく見ることにしましょう。 基本微分と関数のグラフ を参考にしつつ考えていきましょう。 まず、増減を調べる 2つ目は: (g⚪︎f) (x) "3つ"の関数の合成とその手順 (STEP1)まずf (x)とg (x)を合成し、 (STEP2)つぎにその合成関数とh (x)を合成する 逆関数とは 具体例とグラフ・性質 逆関数の求め方2ステップと注意点 step1 (x=)の形にし,xについて解く step2xとyを
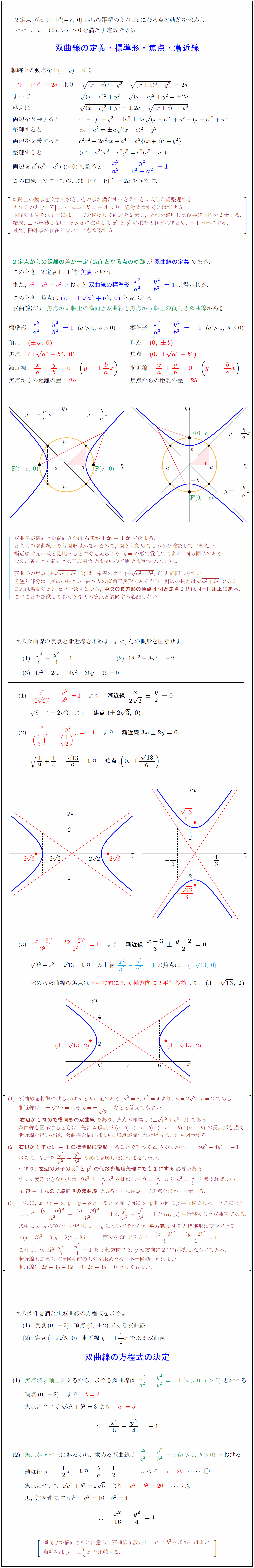



高校数学 双曲線の定義 標準形 焦点 漸近線 双曲線の方程式の決定 受験の月




分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法
対数の定義 課題1 をグラフを用いて考えてみましょう。下に指数関数 \(y = 2^x\) のグラフを描きました。 緑の直線は,図にも示されているとおり \(y = 8\) です。 この直線と \(y = 2^x\) のグラフの交点は,課題1 1 の解を与えています。漸近線 漸近線 有理関数等の水平漸近線,垂直漸近線,斜め漸近線を求める. 関数の漸近線を計算する: (2x^3 4x^2 9)/ (3 x^2) の漸近線 erf (x)の漸近線 方程式で与えられる曲線の漸近線を求める: 漸近線 x^2 y^3 = (x y)^2 もっと表示指数関数のグラフ y = 2x y = 2 x という関数のグラフから、 指数関数の特徴についてを見ていきましょう。 まずは結論から見てしまいましょう。 y = 2x y = 2 x のグラフは以下のようになります。 当然ですが、 y = 2x y = 2 x に、さまざまな数値を入れて計算し
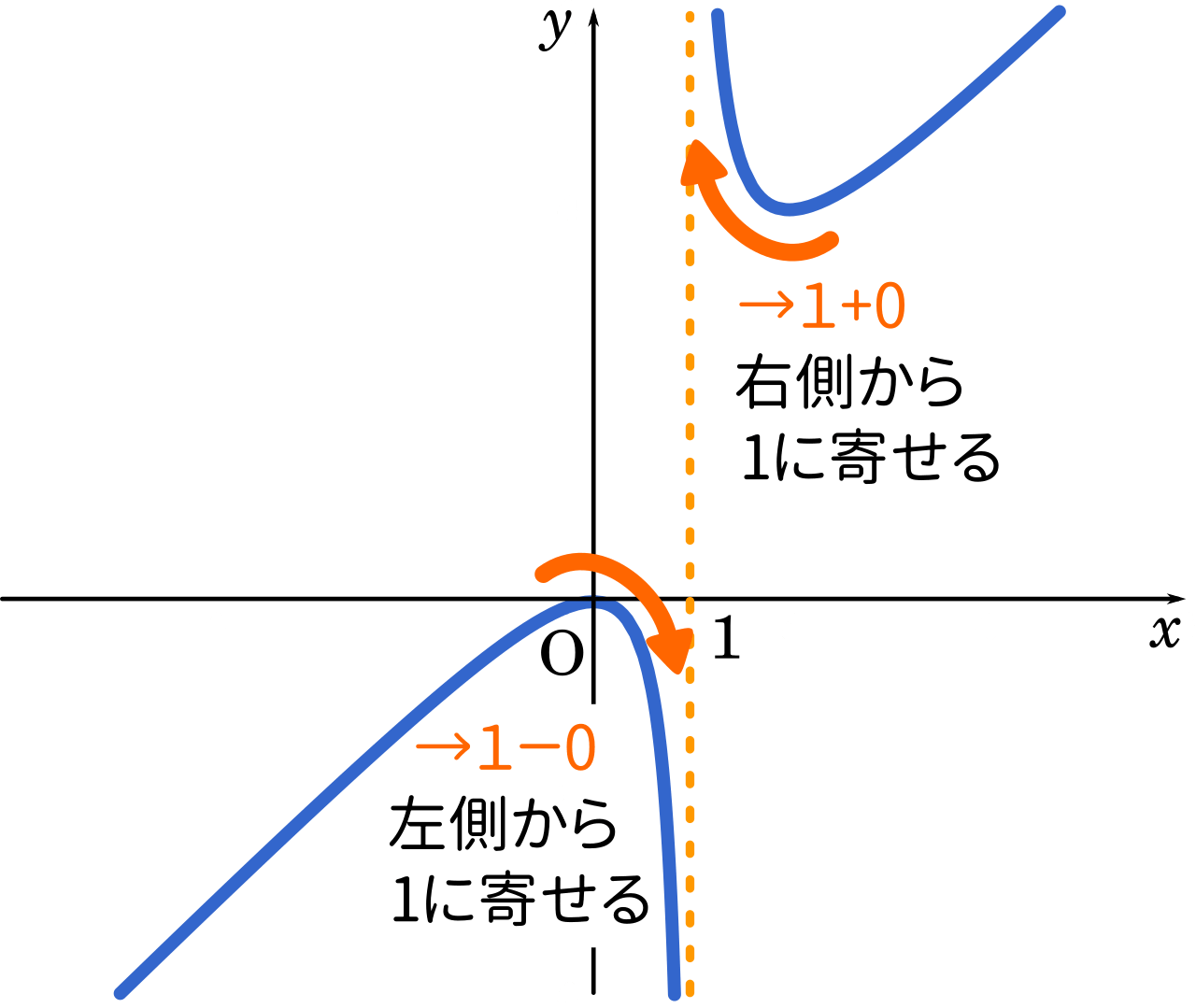



数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



Studydoctor分数関数のグラフの概形 書き方 高校数学 Studydoctor
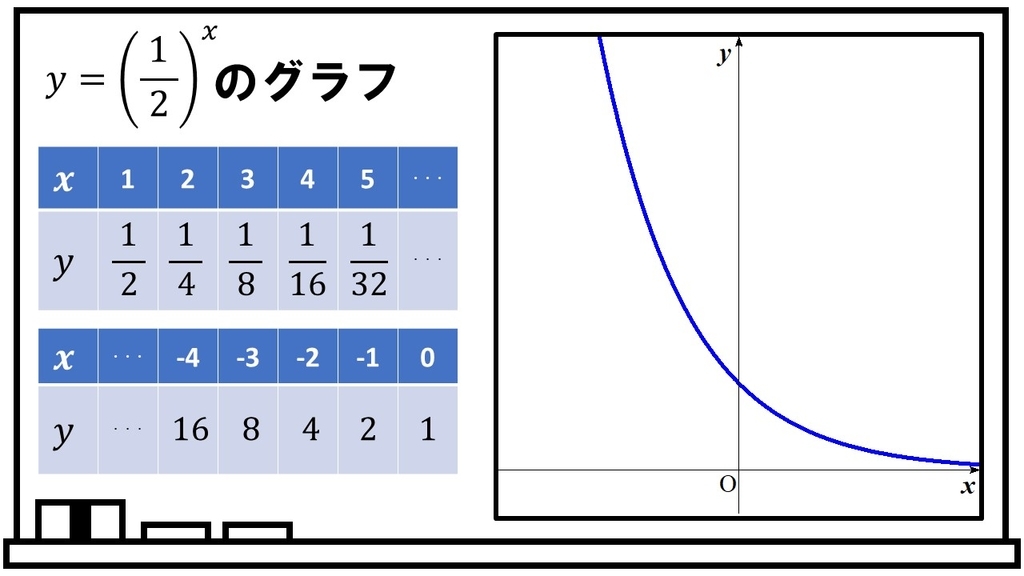
3334 (グラフの準備:漸近線の求め方 (指数対数関数)) 2 1,586 ビュー 見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください. ★の数は優先度です.★→★★→★★★ の順に取り組みましょう. 3241 3352 分数関数の漸近線の求め方について。 分数関数の不連続な点は,分母が0になるときであり, y=x/(x1) においては,x=1です。上図のように指数関数y=a x の漸近線はx軸です(y=a x はx軸に近づく)。指数、累乗の詳細は下記が参考になります。 指数とは?1分でわかる意味、読み方、指数法則、分数との関係 累乗とは?1分でわかる意味、読み方、計算、法則、マイナスとの関係 スポンサーリンク 指数関数の公式と底




漸近線の意味 用法を知る Astamuse



1
数学 漸近線の求めかた?? y=x11/(x1)のグラフを描く問題なんですが、増減表(添付図)を書いた後教科書では次のように漸近線を求めています。 limx→10y=∞, lim 質 微分のとこでグラフ描いてるんですけど漸近線の求め方が分からないです。参考書に書いてある $\displaystyle\lim_{x\rightarrow\infty}\{f(x)(axb)\}=0$ ってどういうこと? 確かにパッと見た目じゃ分からないかもね。それ、いったん置いておいて極限のイメージから漸近線作ってみようか。 ad 増減表を漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。 単元 積分, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め方,log,logarithm> 微分法(iii)複雑な関数のグラフのかき方




標準 一次分数関数の逆関数 なかけんの数学ノート
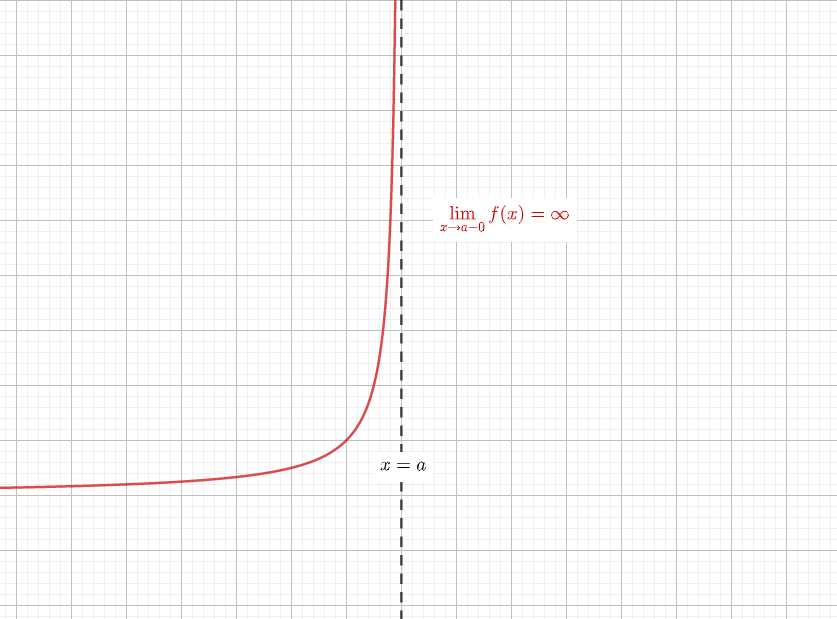



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典



2




指数 対数関数 グラフ編 ますますmathが好きになる 魔法の数学ノート




対数関数とは何か 対数 と 関数 の基礎から応用までを工学博士が解説 Rikeinvest
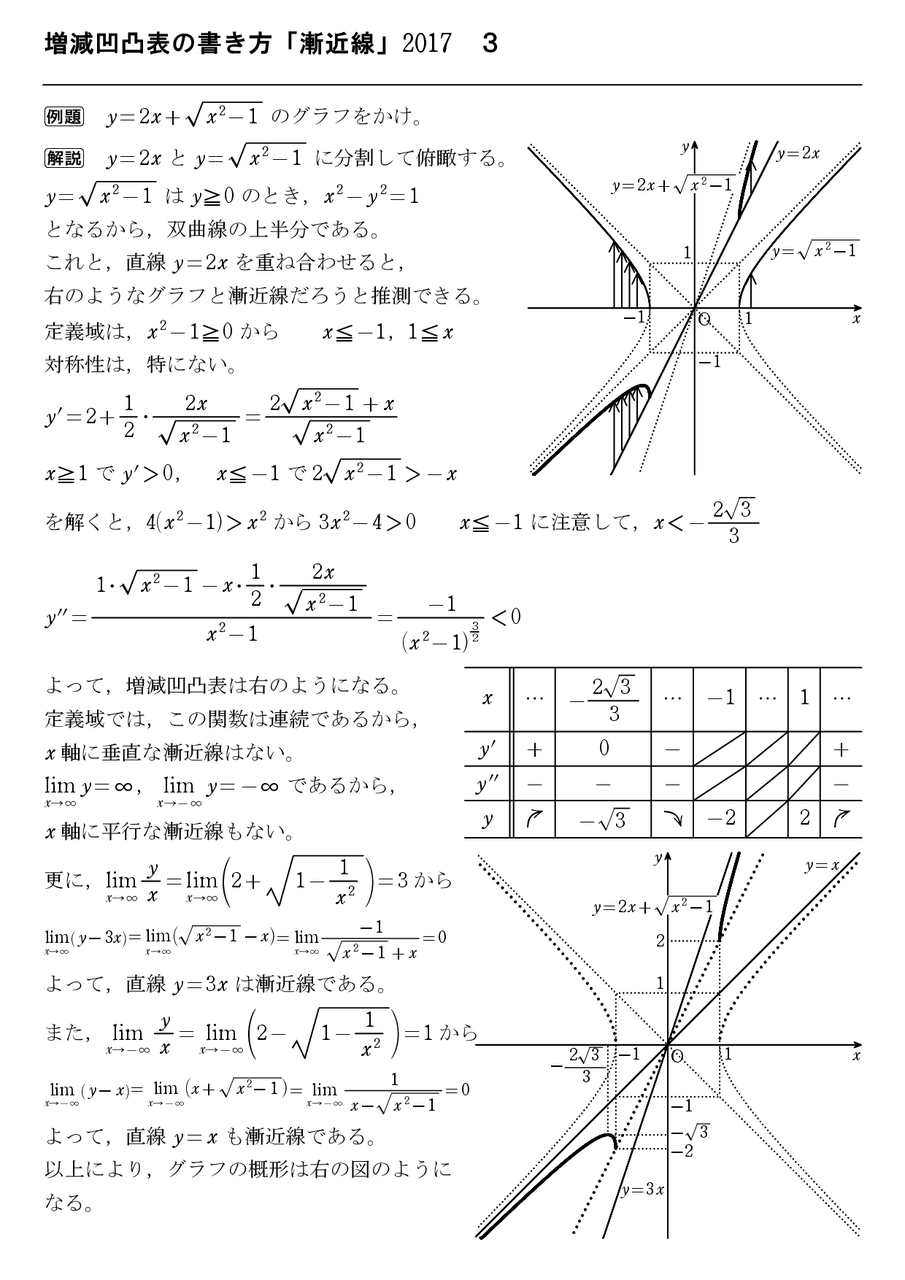



増減凹凸表の書き方 漸近線 17 3 怜悧玲瓏 高校数学を天空から俯瞰する



3




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




数3の グラフの凹凸と変曲点を求める問題での漸近線の求め方が あいうえおって Clearnote



Tikz 高校数学 指数関数とグラフ 数樂管理人のブログ
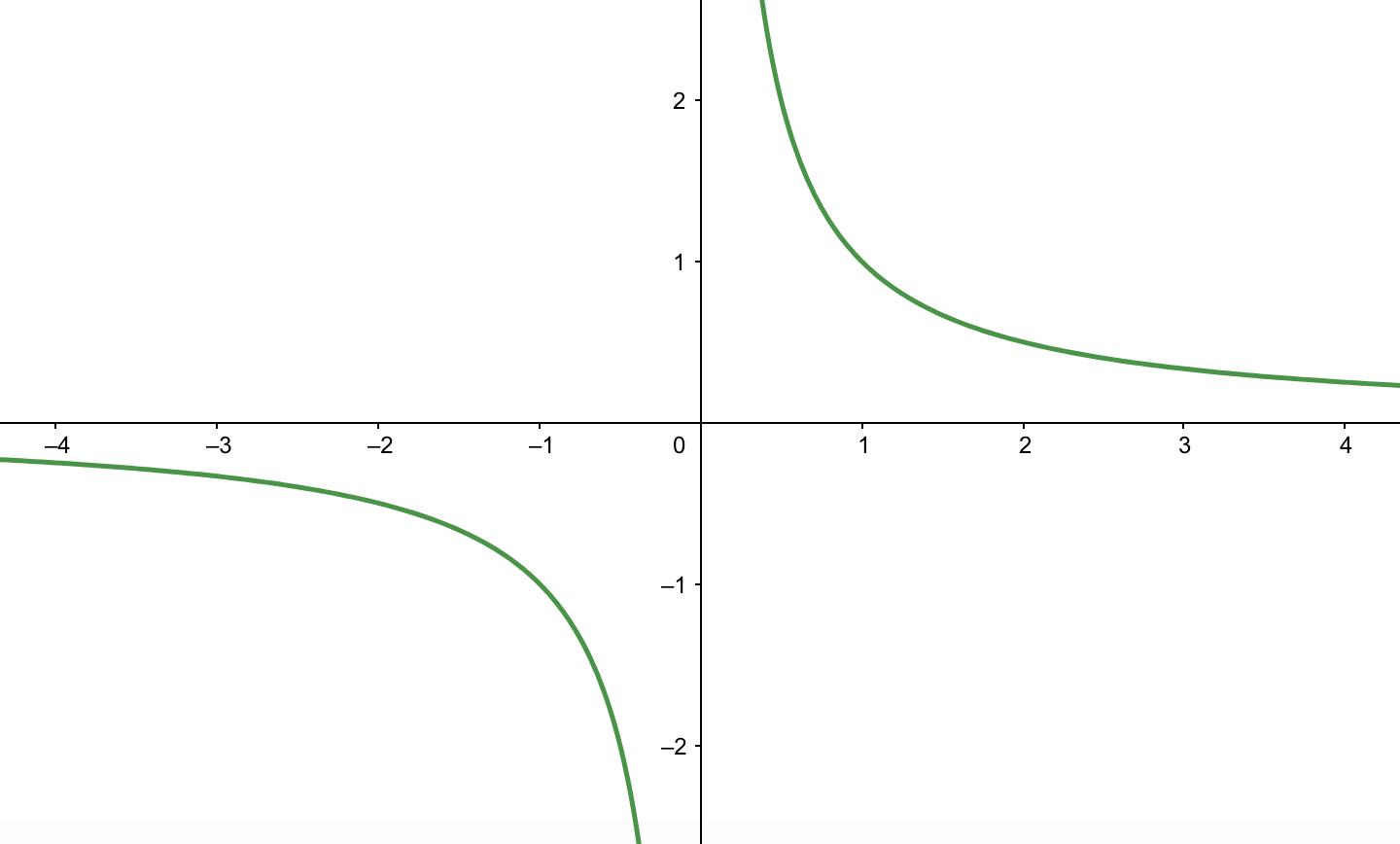



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



指数関数のグラフ 高校数学の無料オンライン学習サイトko Su
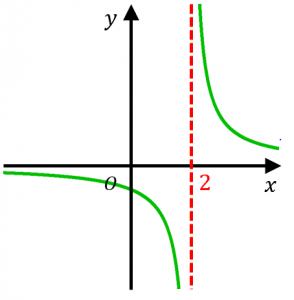



漸近線の求め方3パターン 具体例で学ぶ数学



漸近線 Wikipedia



1




対数関数のグラフと書き方 数学 理系ラボ




指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ
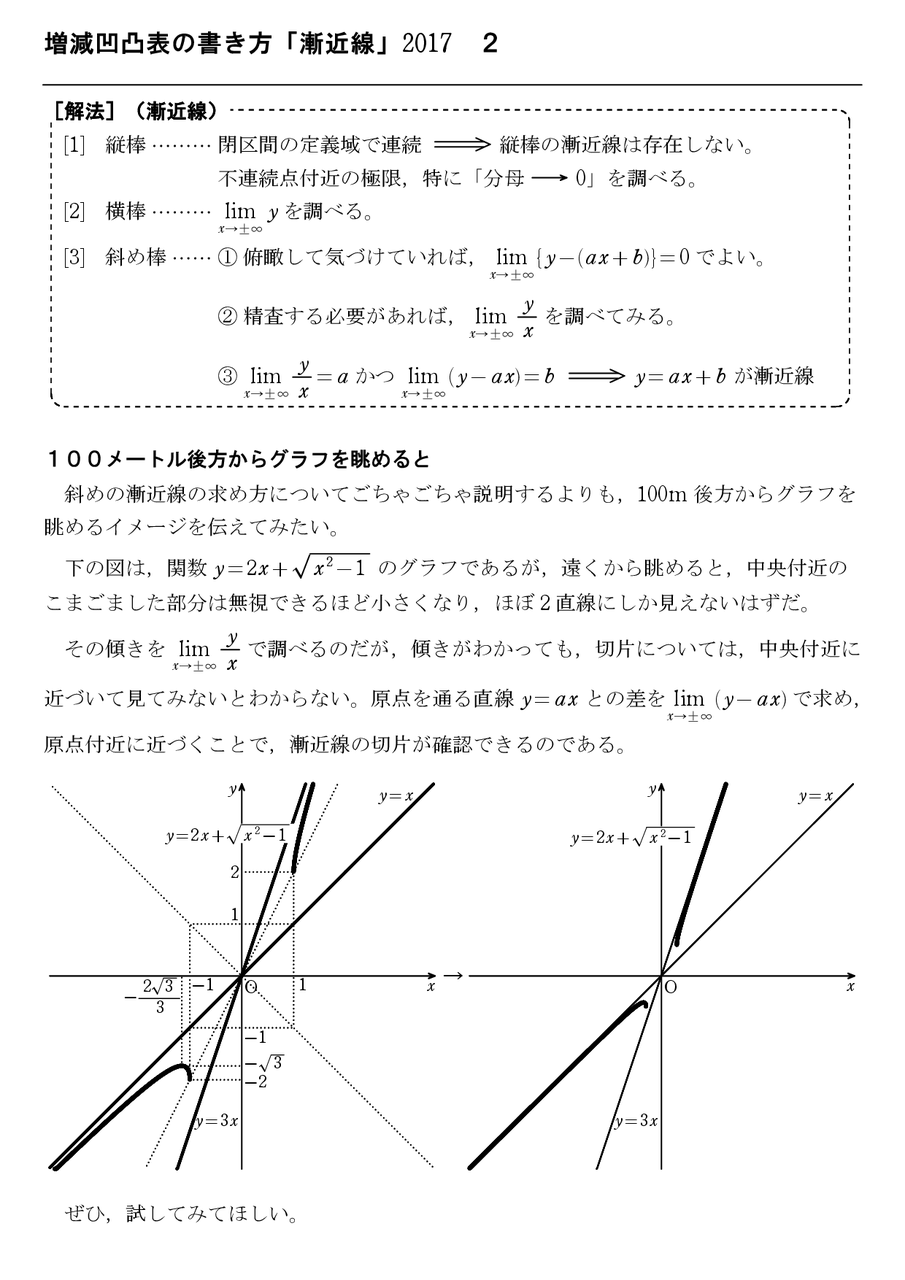



増減凹凸表の書き方 漸近線 17 2 怜悧玲瓏 高校数学を天空から俯瞰する




漸近線 Wikipedia



1



漸近線 Wikiwand




対数関数のグラフと書き方 数学 理系ラボ




一次分数関数のグラフと漸近線 高校数学の美しい物語




漸近線の描き方 一目瞭然早見チャート 高校生 数学のノート Clearnote



2




漸近線の方程式
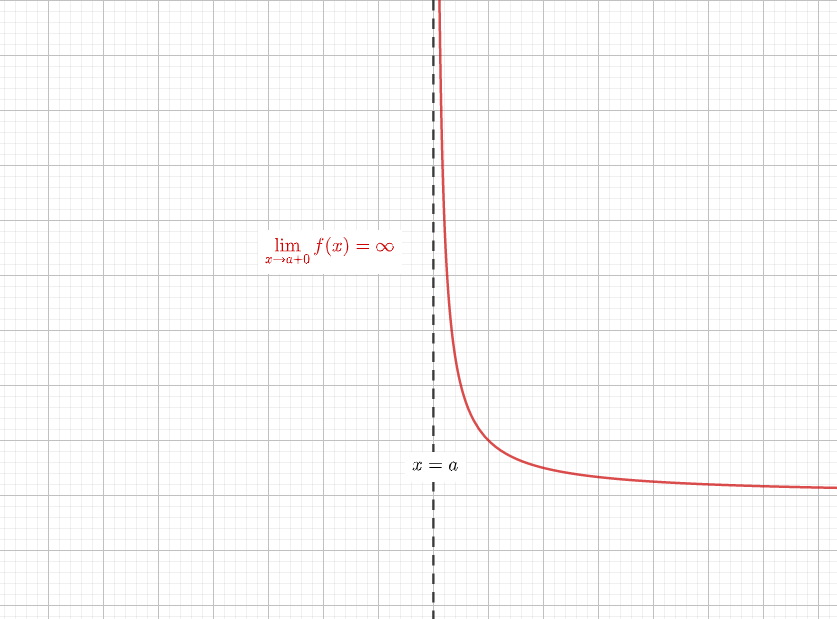



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




対数関数のグラフと書き方3ステップを解説
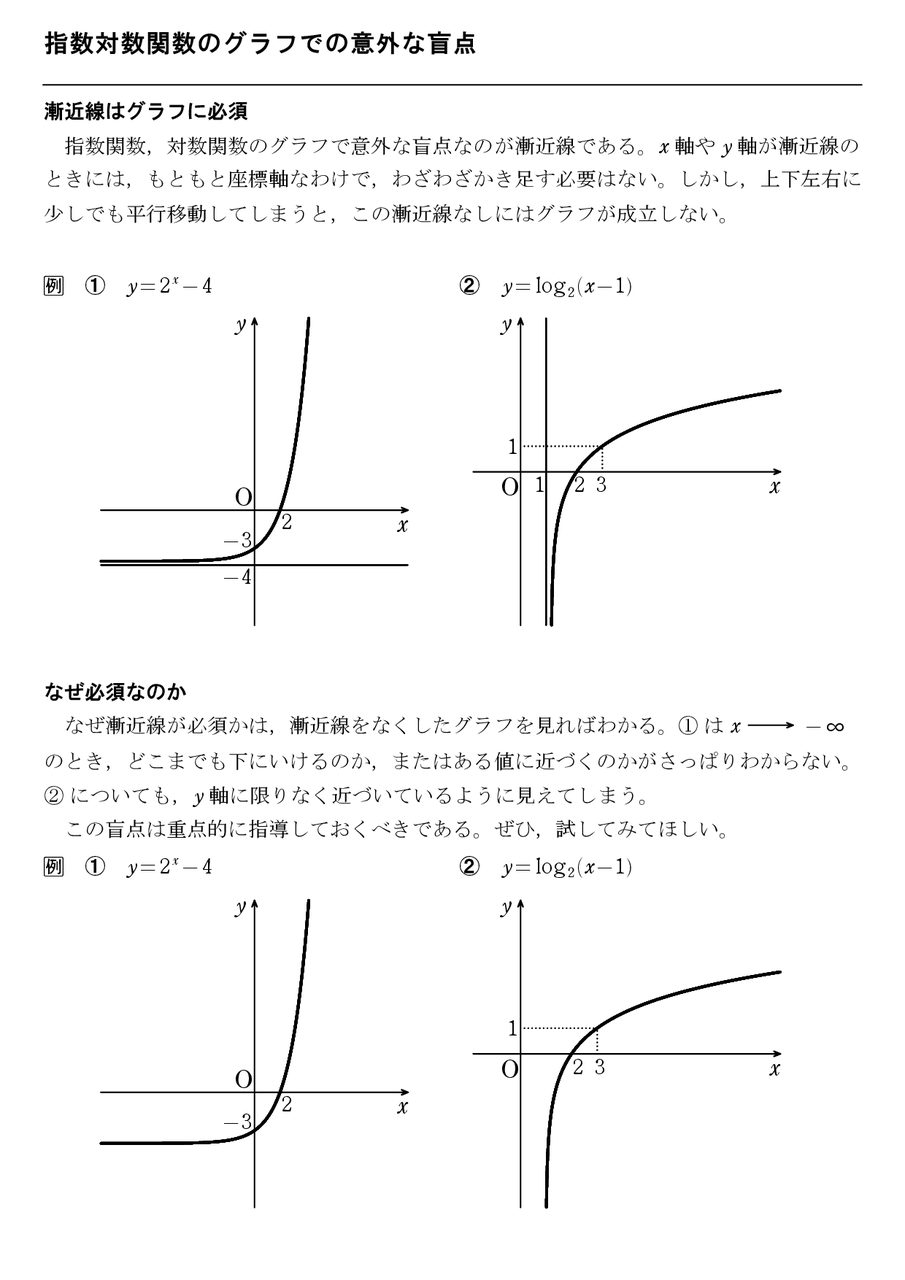



指数対数関数のグラフでの意外な盲点 怜悧玲瓏 高校数学を天空から俯瞰する
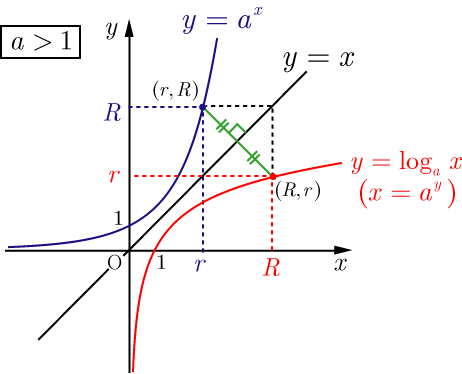



対数関数




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




曲線 漸近線 求め方 2973 曲線 漸近線 求め方 Mbaheblogjpbmo0




基本 双曲線と漸近線 なかけんの数学ノート




高校数学 双曲線のグラフ 1 映像授業のtry It トライイット
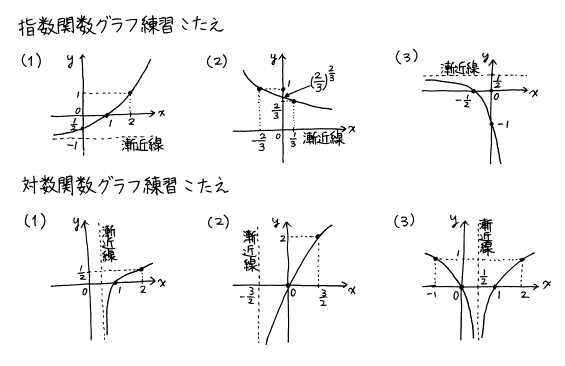



指数関数 対数関数のグラフの解答




漸近線の方程式
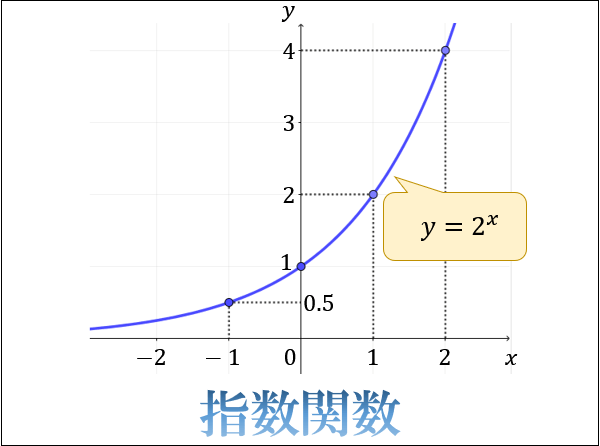



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ




対数関数のグラフと書き方 数学 理系ラボ




漸近線 Wikiwand
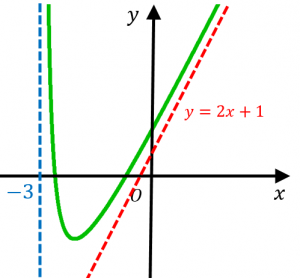



漸近線の求め方3パターン 具体例で学ぶ数学



指数関数とは 1分でわかる意味 公式 底 計算とグラフの関係




対数関数の漸近線の求め方がわかりません Clearnote




漸近線 の新着タグ記事一覧 Note つくる つながる とどける




漸近線 Wikipedia



2



指数関数とは グラフや計算公式 微分積分や方程式 不等式 受験辞典
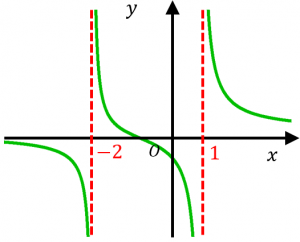



漸近線の求め方3パターン 具体例で学ぶ数学




基礎数学 3回目




漸近線 Wikipedia



指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ




指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




分数関数のグラフの書き方 定義域 漸近線 数学の偏差値を上げて合格を目指す



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



指数関数とは 1分でわかる意味 公式 底 計算とグラフの関係



指数関数のグラフ 指数関数 数学の部屋



Dマイスター 改訂 新数学



漸近線についての質問です 微分のグラフを書くときの漸近線の求め方が分かり Yahoo 知恵袋




指数関数 対数関数のグラフ 数学の偏差値を上げて合格を目指す




標準 微分と関数のグラフと漸近線 なかけんの数学ノート




高校数学 陽関数のグラフの図示の基本的な手順とポイントのまとめ 受験の月
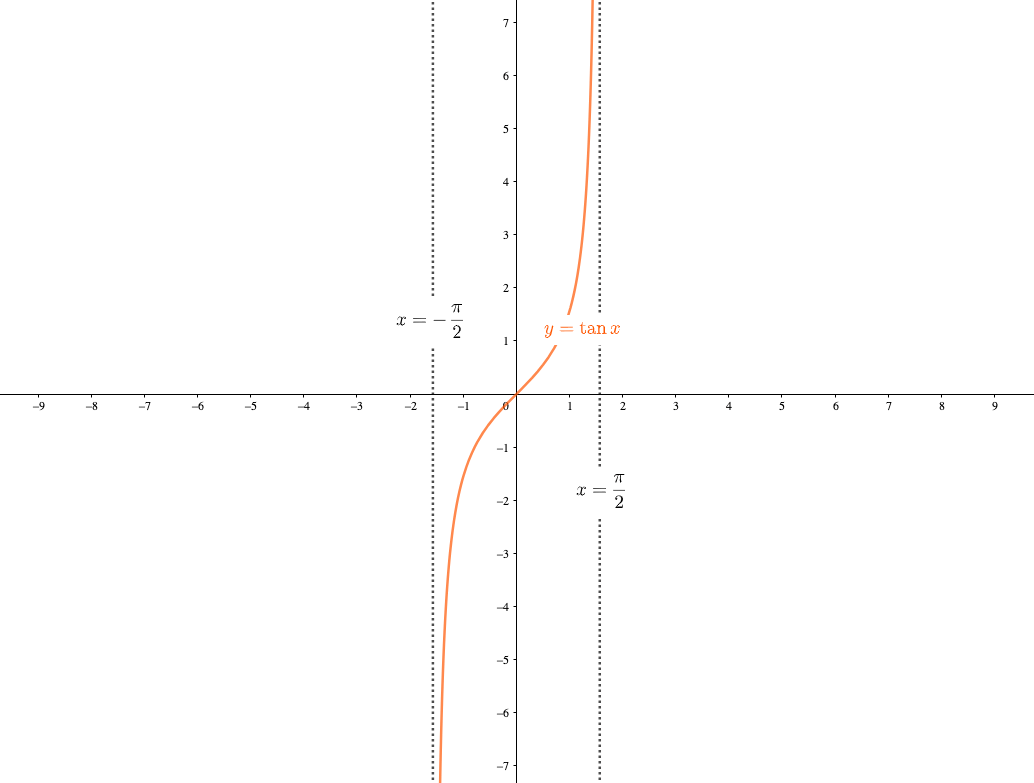



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




数 微分法 漸近線 縦線タイプ オンライン無料塾 ターンナップ Youtube
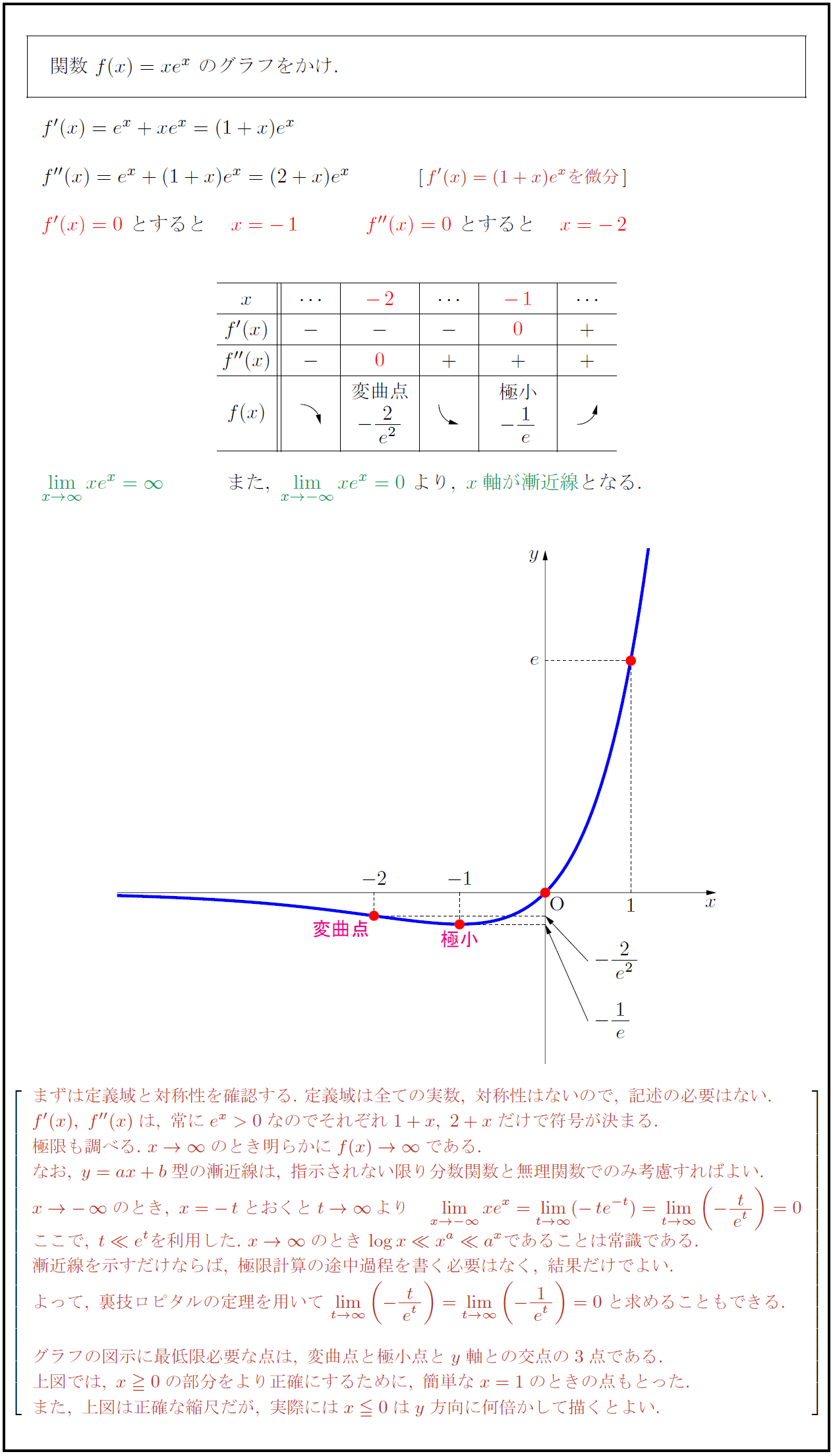



高校数学 指数関数 Y Xe X のグラフ 受験の月



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典




漸近線 Wikiwand




高校数学 分数関数のグラフ 2 映像授業のtry It トライイット




漸近線 の限界に漸近してみる Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー




一次分数関数のグラフと漸近線 高校数学の美しい物語



指数関数のグラフ



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



数3微分の応用について質問です 曲線の概形をかけという問題で Yahoo 知恵袋




双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語
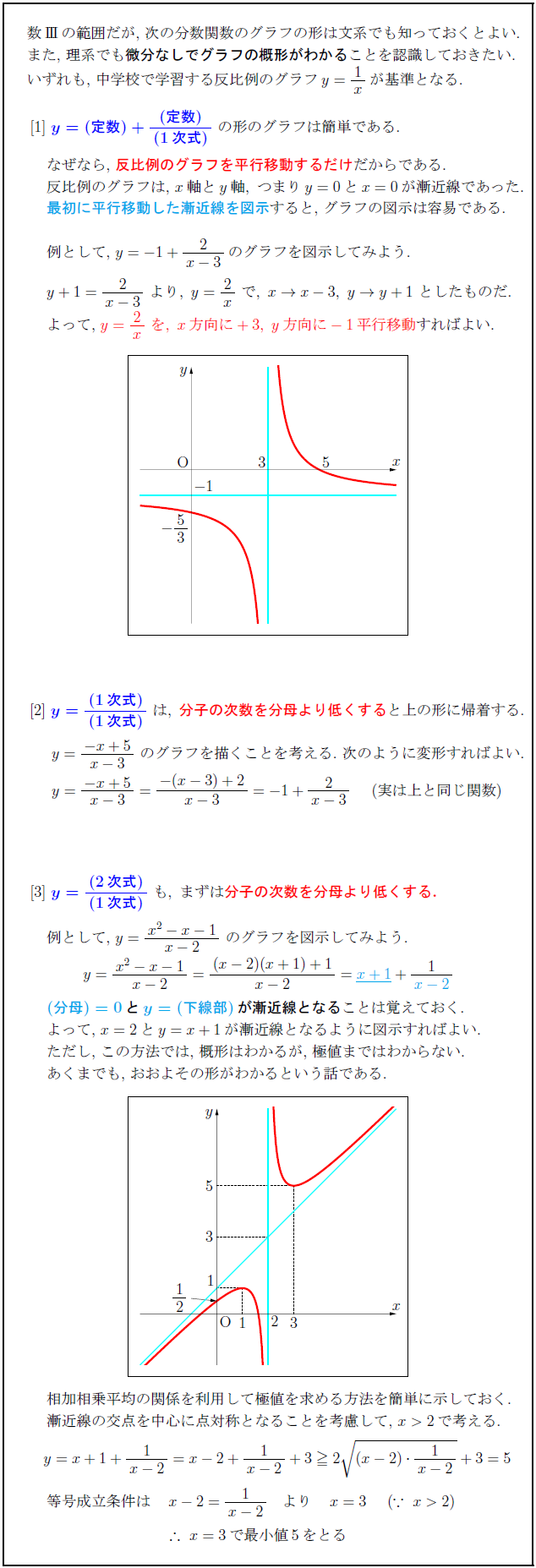



高校数学 文系も知っておくべき基本的な分数関数 数 のグラフ 受験の月




対数関数のグラフと書き方 数学 理系ラボ




画像の 5 の指数関数はどうやってグラフを書く Okwave
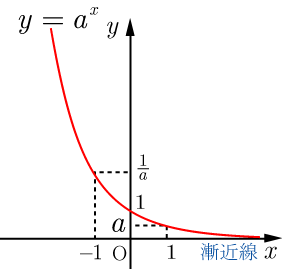



指数関数



漸近線について 指数のグラフで漸近線は必要でしょうか Yahoo 知恵袋



指数関数とは グラフや計算公式 微分積分や方程式 不等式 受験辞典
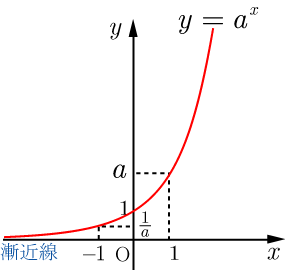



指数関数
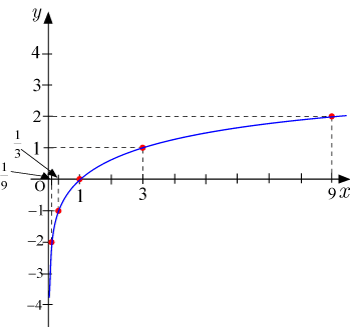



基本的な対数関数のグラフ
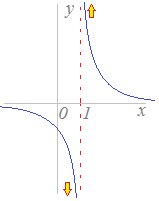



漸近線の方程式




対数関数のグラフと書き方3ステップを解説



漸近線についての質問です 微分のグラフを書くときの漸近線の求め方が分かり Yahoo 知恵袋
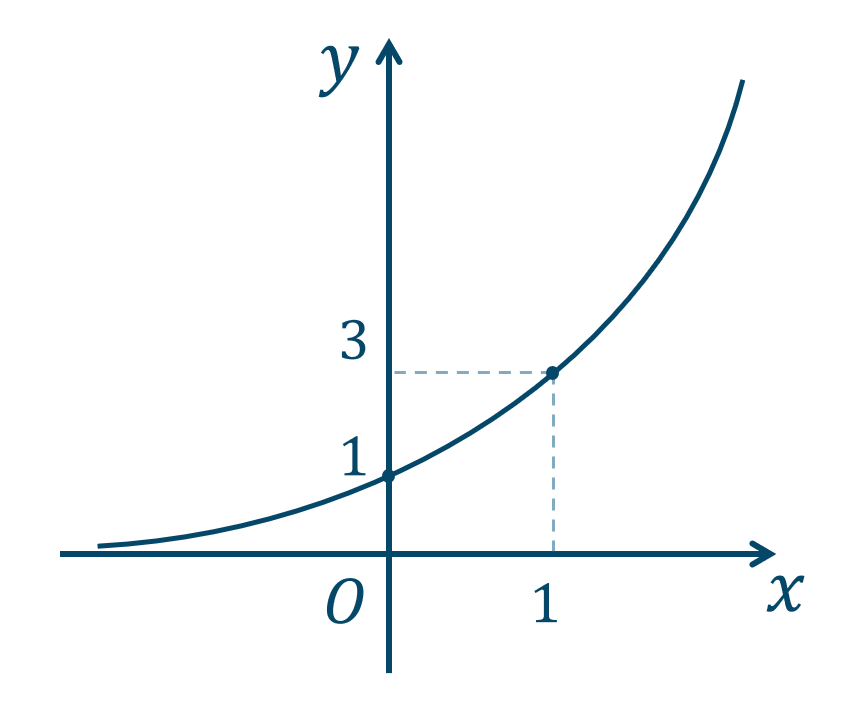



数学 指数関数のグラフの描き方とコツ ページ 2 教科書より詳しい高校数学
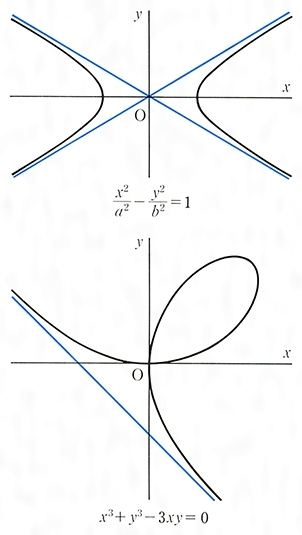



漸近線とは コトバンク




数3微分のグラフについてです この問題の漸近線の求め方が分かりません Clearnote




高校数学 分数関数のグラフ 1 映像授業のtry It トライイット




対数関数の漸近線の求め方がわかりません Clearnote



0 件のコメント:
コメントを投稿